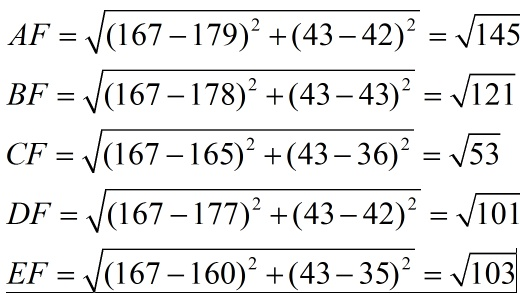Hi，大家好，我是编程小6，很荣幸遇见你，我把这些年在开发过程中遇到的问题或想法写出来，今天说一说KNN（k近邻详解）,希望能够帮助你!!!。

KNN（k近邻详解）

详细链接一
详细链接二

一句话说明白KNN算法原理

下面我们只讲关于分类的KNN，回归的不讲。

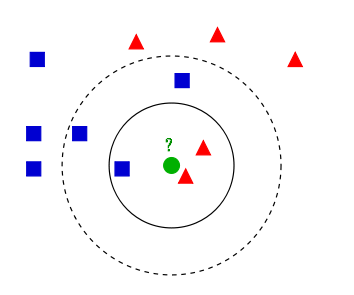
其实很简单，就是计算你要预测的点的周围最近的K个点，然后取这k个点中最多的类定义为你要预测的这个点所属的类型。如下图所示，比如说：
有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的，来了一个新的数据点，我要得到它的类别是什么？好的，下面我们根据k近邻的思想来给绿色圆点进行分类。
1、如果K=3，绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
2、如果K=5，绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

这就是KNN算法，很简单吧。那我们就来详细解决上述算法中的一些遗留问题。

1、最近的距离度量怎么计算？

有下面这几种计算方式：

但是光有这些还不够，还必须有特征归一化。你比如说：

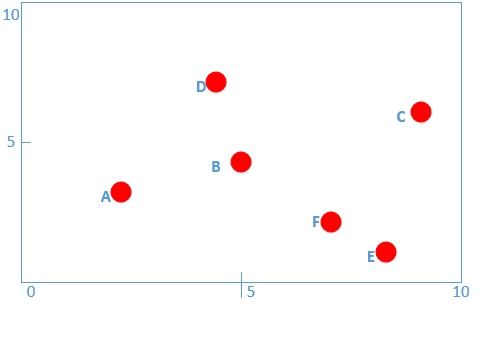
首先举例如下，我用一个人身高(cm)与脚码（尺码）大小来作为特征值，类别为男性或者女性。我们现在如果有5个训练样本，分布如下：

A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]

通过上述训练样本，我们看出问题了吗？

很容易看到第一维身高特征是第二维脚码特征的4倍左右，那么在进行距离度量的时候，我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的，最终可能会导致距离计算错误，从而导致预测错误。口说无凭，举例如下：

现在我来了一个测试样本 F(167,43)，让我们来预测他是男性还是女性，我们采取k=3来预测。

下面我们用欧式距离分别算出F离训练样本的欧式距离，然后选取最近的3个，多数类别就是我们最终的结果，计算如下：

由计算可以得到，最近的前三个分别是C,D,E三个样本，那么由C,E为女性，D为男性，女性多于男性得到我们要预测的结果为女性。

这样问题就来了，一个女性的脚43码的可能性，远远小于男性脚43码的可能性，那么为什么算法还是会预测F为女性呢？那是因为由于各个特征量纲的不同，在这里导致了身高的重要性已经远远大于脚码了，这是不客观的。所以我们应该让每个特征都是同等重要的！这也是我们要归一化的原因！
归一化公式如下：

2、K值的选取

还有一个最大的问题，K怎么选？？？
选的太小的话，会造成过拟合，选的太大的话，会造成模型太简单，无法起到分类的作用。

那么我们一般怎么选取呢？李航博士书上讲到，我们一般选取一个较小的数值，通常采取 交叉验证法来选取最优的k值。（也就是说，选取k值很重要的关键是实验调参，类似于神经网络选取多少层这种，通过调整超参数来得到一个较好的结果）

简单地说就是调超参吧。

3、K近邻算法的实现：KD树的原理讲解

kd 树的结构

kd树是一个二叉树结构，它的每一个节点记载了【特征坐标，切分轴，指向左枝的指针，指向右枝的指针】。

其中，特征坐标是线性空间 Rn 中的一个点 (x1,x2,…,xn)切分轴由一个整数 r 表示，这里 1≤r≤n，是我们在 n 维空间中沿第 rr维进行一次分割。节点的左枝和右枝分别都是 kd 树，并且满足：如果 y 是左枝的一个特征坐标，那么 yr≤xr（左分支结点）；并且如果 z 是右枝的一个特征坐标，那么 zr≥xr（右分支结点）。

给定一个数据样本集 S⊆Rn 和切分轴 r，以下递归算法将构建一个基于该数据集的 kd 树，每一次循环制作一个节点：
−− 如果 |S|=1，记录 S 中唯一的一个点为当前节点的特征数据，并且不设左枝和右枝。（|S| 指集合 S 中元素的数量）
−− 如果 |S|>1

1、将 S 内所有点按照第 r 个坐标的大小进行排序；
2、选出该排列后的中位元素（如果一共有偶数个元素，则选择中位左边或右边的元素，左随便哪一个都无所谓），作为当前节点的特征坐标，并且记录切分轴 r；
3、将 SL设为在 S 中所有排列在中位元素之前的元素； SR 设为在 S 中所有排列在中位元素后的元素；
4、当前节点的左枝设为以 SL 为数据集并且 r 为切分轴制作出的 kd 树；当前节点的右枝设为以 SR 为数据集并且 r为切分轴制作出的 kd 树。再设 r←(r+1)modn。（这里，我们想轮流沿着每一个维度进行分割；modn 是因为一共有 n 个维度，在沿着最后一个维度进行分割之后再重新回到第一个维度。）

如果没看懂很正常，简单地来说，先将你的训练数据按照第一维排序，然后取中位数的那个数据x，根据x把数据集分为左右两部分，然后再分别对左右两部分按照第二维取中位数分割，就这样迭代下去，直到最后一维。

如果你还是不懂，看一个例子。

给定一个二维空间的数据集：

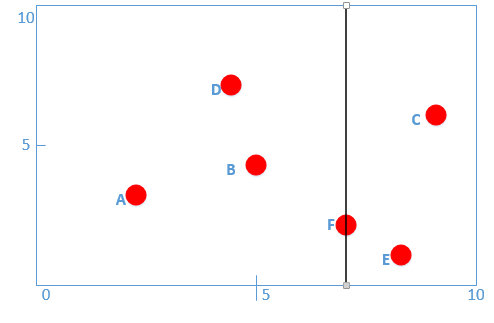
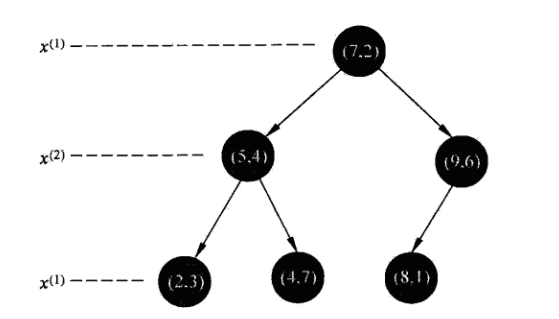
T = {（2,3），（5,4），（9,6）,（4,7），（8,1），（7,2）}， 构造一个平衡kd树。

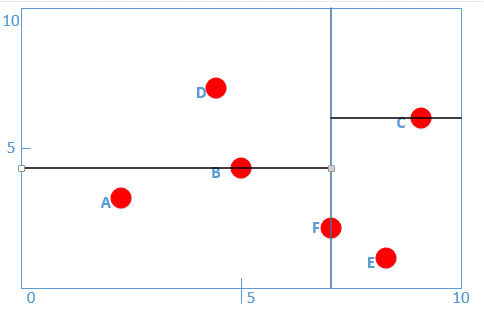
为了方便，我这里进行编号A(2，3)、B（5,4）、C（9,6）、D（4,7）、E（8,1）、F（7,2）

初始值r=0，对应x轴。

首先先沿 x 坐标进行切分，我们选出 x 坐标的中位点，获取最根部节点的坐标，对数据点x坐标进行排序得：

A(2，3)、D（4,7）、B（5,4）、F（7,2）、E（8,1）、C（9,6）

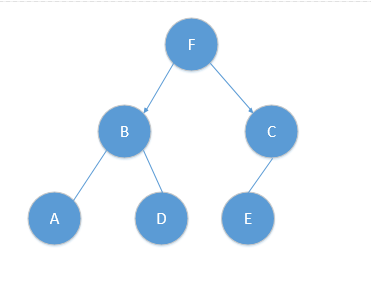
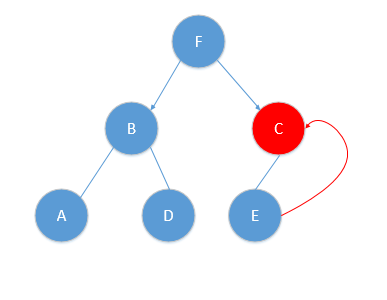
则我们得到中位点为B或者F，我这里选择F作为我们的根结点，并作出切分（并得到左右子树），如图：

对应的树结构如下：

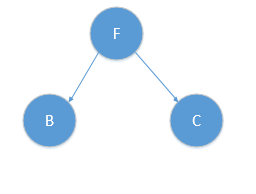
根据算法，此时r=r+1=1，对应y轴，此时对应算法|S|>1，则我们分别递归的在F对应的左子树与右子树按y轴进行分类，得到中位节点分别为B，C点，如图所示：

对应树结构为：

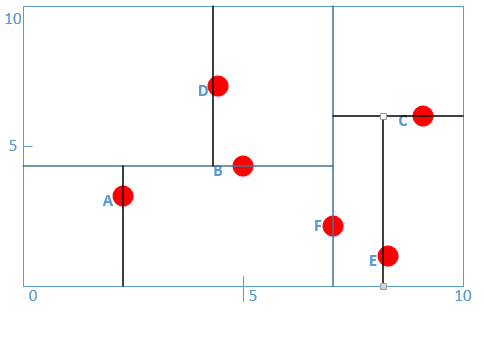
而到此时，B的左孩子为A，右孩子为D，C的左孩子为E,均满足|S|==1，此时r = (r+1)mod2 = 0,又满足x轴排序，对x轴划分！则如图所示：

对应树结构如下：

kd树的搜索
输入：已构造的kd树；目标点x；

输出：x的最近邻.

（1）在kd树中找出包含目标点x的叶结点：从根结点出发，递归地向下访问kd树，若目标点x当前维的坐标小于切分点的坐标,则移动到左子节点，否则移动到右子结点.直到子结点为叶结点位置.

（2）以此叶结点为“当前最近点”

（3）递归地向上回退，在每个结点进行以下操作：

（a）如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”.

（b）当前最近点一定存在于该结点一个子结点对应的区域.检查该子结点的父结点的另一个子结点对应的区域是否有更近的点.具体地，检查另一子结点对应的区域是否以目标点为球心、以目标点与“当前最近点”间为半径的超球体相交。

如果不相交，向上回退.

（4）当回退到根结点时，搜索结束。最后的“当前最近点”即为最近邻点.

看到这里是不是有点晕了，哈哈，不要怕，下面通过例子，一步一步走一遍上面所描述的算法过程，化抽象为具体！

kd树最近邻搜索例题：

给定一个二维空间的数据集：

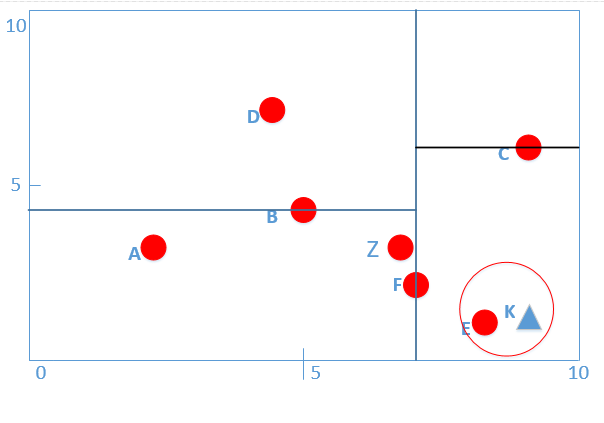
T = {（2,3），（5,4），（9,6）,（4,7），（8,1），（7,2）}，输入目标实例为K(8.5,1),求K的最近邻。

首先我们由上面可以给出，T的kd树对应如下：

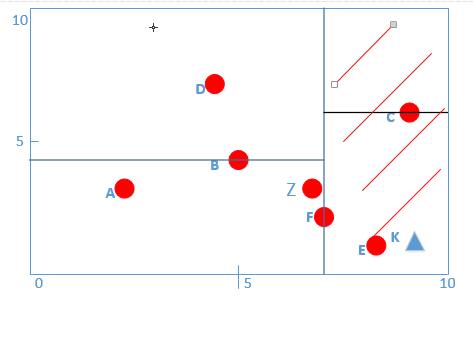
我们此时的K（8.5,1），根据算法第一步得：第一层的x轴K点为8大于F点的7，所以进入F（7,2）的右子树，进入下面红色线条区域：

到了第二层，分割平面坐标为y轴，K点y轴坐标为1，小于C点y轴坐标6，则继续向右走，在下图红色线条区域内：

则此时算法对应第（1）部分完成，我们找到了叶子节点E（8,1）。

我们进行算法第（2）步，把E（8,1）作为最近邻点。此时我们算一下KE之间的距离为0.5（便于后面步骤用到）.

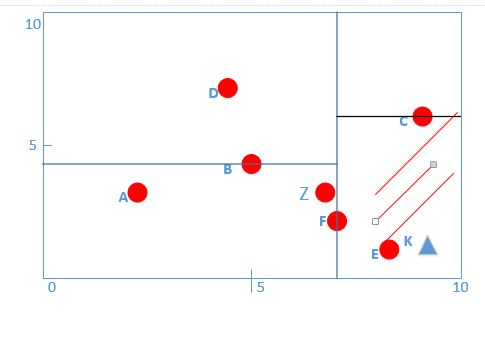
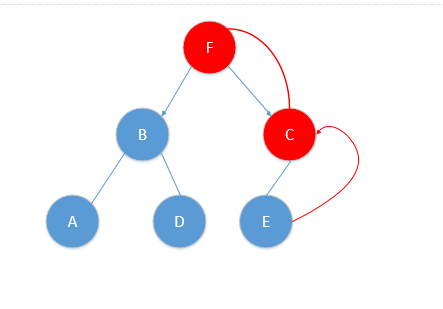
然后进行算法第（3）步，递归的往上回退，每个结点进行相同步骤，好，我现在从E点回退到C点，对应图片如下；

此时对C点进行第（3）步的（a）操作，判断一下KC距离与保存的最近邻距离（这时是KE）比较，KC距离为点K（8.5,1）与点C（9,6）之间的距离√25.25>最近邻0.5，于是不更新最近邻点。

然后对C点进行第（3）步的（b）操作，判断一下当前最近邻的距离画一个圆是否与C点切割面相交，如图所示：

们很容易看到与C点切割面并没有相交，于是执行由C点回退到它的父结点F点。如图：

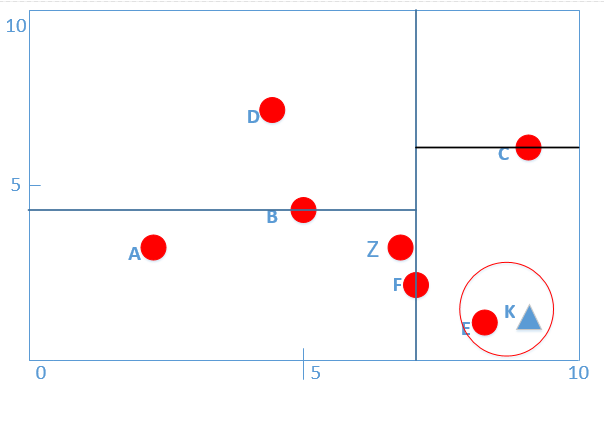
对F点进行（a），（b）操作！

进行（a）步骤，判断FK的距离是否小于当前保存的最小值，FK=√1.25>0.5,所以不改变最小距离

下面我们进行（b）步骤，为了判断F点的另一半区域是否有更小的点，判断一下当前最近邻的距离画一个圆是否与F点切割面相交，如图所示：

发现与任何分割线都没有交点，那么执行算法最后一步，此时F点已经是根结点，无法进行回退，那么我们可以得到我们保留的当前最短距离点E点就是我们要找的最近邻点！任务完成，
并且根据算法流程，我们并没有遍历所有数据点，而是F点的左孩子根本没有遍历，节省了时间，但是并不是所有的kd树都能到达这样的效果。

总结

1.我们提出了k近邻算法，算法的核心思想是，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。更通俗说一遍算法的过程，来了一个新的输入实例，我们算出该实例与每一个训练点的距离（这里的复杂度为0(n)比较大，所以引出了下文的kd树等结构），然后找到前k个，这k个哪个类别数最多，我们就判断新的输入实例就是哪类！

2.与该实例最近邻的k个实例，这个最近邻的定义是通过不同距离函数来定义，我们最常用的是欧式距离。

3.为了保证每个特征同等重要性，我们这里对每个特征进行归一化。

4.k值的选取，既不能太大，也不能太小，何值为最好，需要实验调整参数确定！
5、kd树的建立以及搜索。

K近邻的优缺点

优点：

1.KNN分类方法是一种非参数的分类技术，简单直观，易于实现！只要让预测点分别和训练数据求距离，挑选前k个即可，非常简单直观。

2.KNN是一种在线技术，新数据可以直接加入数据集而不必进行重新训练

缺点及改进：

1.当样本不平衡时，比如一个类的样本容量很大，其他类的样本容量很小，输入一个样本的时候，K个邻近值大多数都是大样本容量的那个类，这时可能会导致分类错误。

改进方法：对K邻近点进行加权，也就是距离近的权值大，距离远的点权值小。

2.计算量较大，每个待分类的样本都要计算它到全部点的距离，根据距离排序才能求得K个临近点。

改进方法：先对已知样本带你进行裁剪，事先去除分类作用不大的样本，采取kd树以及其它高级搜索方法BBF等算法减少搜索时间。

今天的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。