博弈论
博弈论是现代数学的一个分支,是用于研究竞争现象的数学工具。博弈策略是一套考虑到所有可能的情况而做出的行动。博弈论在人工智能方面有极大的价值。
零和博弈
在零和博弈,双方的总利益为0,其中一方为了自己利益最大化,必须损失另一方的利益。正如棋局中,一方赢了,则另一方必定输了,则利益之和为 1+(-1)=0
这就要求,任意一方都要使自己利益最大化,同时使对方利益最小化。因此在决策时,不能只考虑自己的最大利益,还需要考虑对方做出的对自己最不利的选择
极大极小策略
极大极小方法是分析零和博弈问题时的一种策略,在对局制游戏中,每个参与者都会做出对自己最有利,同时也是对对方最不利的选择。
在下棋时,每一个棋盘布局都可以表示为一个节点,相邻的节点形成多叉树。每种布局都会对一方有利而对另一方不利,称节点的有利程度为价值。
假设人类与计算机进行对决,并假设人类绝对聪明,那么在人类的回合,他会选择对计算机最不利的棋局,也人工智能基础java就是价值最低的节点。而计算机则会选择对自己价值最高的节点。
假设各节点的价值如下
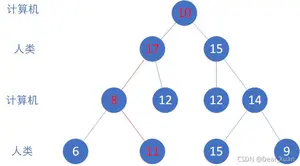
决策过程如下:
- 计算机选择对自己有利的节点:10→17
- 人类选择对计算机不利的节点:17→8
- 计算机选择对自己有利的节点:8→11
- 人类…… 称这种在最大和最小值之间不断切换的决策过程为极大极小策略
这是一种保守策略,因为计算机不会尝试冒险,它会假设人类每次都做出对自己最不利的选择,从而保证自己最后得到节点价值不至于太低
井字棋算法
棋局
用TicTac类表示棋局,用数组保存棋子
回合
用节点表示一个回合,节点包括棋局,价值,子节点,棋手,落子位置
其中子节点包含了当前回合后所有可能的情况,棋手是当前回合轮到的棋手,落子位置是上一回合的棋手下的最后一步棋位置
棋局价值
对于一种棋局,如果游戏已经结束,那么根据获胜者来计算价值。如果获胜者为电脑,则价值为10;如果获胜者为人类,则价值为-10;如果平局,则价值为0
如果游戏尚未结束,则在棋局上所有空位置落子,并得到所有可能的子节点。如果当前棋手是人类,则该节点的价值是子节点的价值的最小值,因为人类会做出对计算机最不利的选择。如果当前棋手是电脑,则该节点的价值是子节点的价值的最大值,因为电脑会做出对自己最有利的选择。
下棋代码
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/h6javajc/20141.html
