
大家好呀,今天,
小编给大家带来的的二叉树的理论知识的讲解,
和一些常考的面试题~
树和二叉树的性质:
1. 树型结构:
概念:
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合.
像一棵倒挂的树
树是根朝上,而叶朝下的。
树的特点:
- 有一个特殊的结点,称为根结点
- 根结点没有前驱结点
- 其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm
- 每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树
- 每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。
如下图,就是一个树:
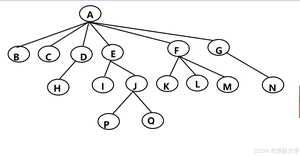
树的性质(黄色部分为重点内容, 黑色部分为了解内容):
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等节点为叶结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等节点为分支结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
二叉树:
二叉树的结构:
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成
二叉树的特点:
- 二叉树没有度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒
- 二叉树是有序树
需要注意的是,以下的树也是二叉树哦:
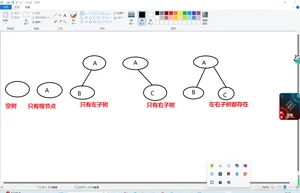
特殊的二叉树:
满二叉树:
每层的节点个数达到最大值的是满二叉树
若满二叉树的层数是K层,则节点总数
是2^k -1 个
对于任何一颗二叉树,叶子结点的个数永远比度为2的节点的个数多一
我们现在假设n0 是度为0的节点也就是叶子结点
n1是度为1的节点
n2是度为2的节点
那么二叉树的总节点的个数就是:
总节点 = n0 + n1 + n2;
关于二叉树的性质
叶子结点的个数等于度为2的节点的个数加一
一颗n个结点的树有n-1条边
那么在完全二叉树中
如果总节点的个数是偶数:则n1 = 1;
如果总结点的个数是奇数,则n1 = 0
如图:
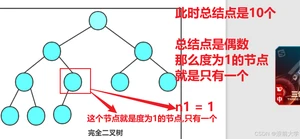
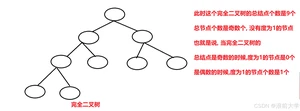
所以可以得出以下结论:
在完全二叉树中:
总节点的个数是偶数:则n1 = 1;
总结点的个数是奇数,则n1 = 0
好啦,以上就是二叉树的基本性质啦
那我们了解了这些二叉树的性质之后
我们能够干什么呢?
当然是去做题啦!!!
接下来:
各位选手,请听题:
例题:
在具有2n个节点的完全二叉树中,叶子结点的个数是多少个?
(叶子结点就是n0的个数)
各位选手,请作答~
正确答案往后翻阅即可~
好啦,相信你已经通过自己的头脑风暴,做出来了
那就一起来看看小编的解题思路吧~
题目解析如下:
总结点的个数= n0 + n1 + n2;
所以:
2n = n0 + n1 + n2;
n0 = n2 + 1;
n2 = n0 - 1;
2n = n0 +n1 + n0 -1;
由于这个完全二叉树的总结点的个数是2n个,总结点的个数一定是偶数
所以这个完全二叉树的n1的个数是1
所以:
2n = n0 + n1 + n0 - 1 ;
2n = n0 + 1 + n0 - 1;
2n = 2n0 ;
n = n0;
所以:
在具有2n个节点的完全二叉树中,叶子结点的个数是多少个
叶子节点的个数是n个
例题2:
一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
选哪一个呢?
俺的解析如下:
767 = n0 +n2;
n0 = n2 +1;
n2 = n0 - 1;
767 = n0 + n0 - 1;
768 = 2n0;
n0 = 384;
选B…
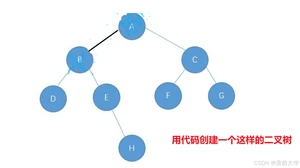
用代码创建一个二叉树:
我们会使用代码创建一个如图所示的二叉树
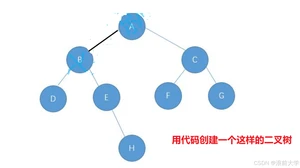
测试用例如下:
代码分析如下:
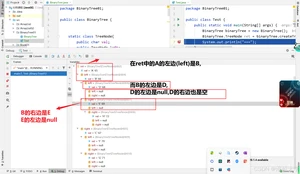
二叉树的遍历方式:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
前序遍历: ( 根->左->右)
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树
每一颗树的遍历都是以同样的方式进行遍历的( 根->左->右)(包括左子树和右子树)
树是递归定义的
中序遍历:(左->根-> 右)
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
每一颗树的遍历都是以同样的方式进行遍历的( 左-> 根->右)
后序遍历(左->右->根)
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点
每一颗树的遍历都是以同样的方式进行遍历的( 左-> 右->根)
层序遍历
从上到下,从左到右依次遍历~
例题1:写出下图的三种遍历方式:
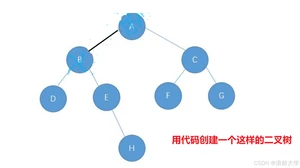
前序遍历: 根->左->右: A B D E H C F G
中序遍历: 左->根->右: D B E H A F C G
后序遍历: 左->右->根: D H E B F G C A
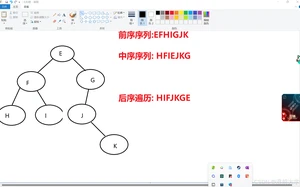
例题2:
解答入下:
我们可以得知:E是二叉树的根结点
HFI在根结点的左边
JKG在根结点的右边
根结点的左边就是左子树,右边就是右子树
再根据遍历序列可以得出:
如图所示:
例题3:
一个二叉树的前序遍历序列{1,2,4,7,3,5,6,8}, 中序遍历序列{4,7,2,1,5,3,8,6}, 请重建二叉树以及写出后序遍历序列:
方法和上面那题一样的~
先找出根节点
再根据中序序列找出根结点的左边和右边…
根结点的左边就是左子树,右边就是右子树
小伙伴们,可以自己尝试一下
看看做完之后,可以和俺对一对答案~
话不多说, 咱们直接上图:
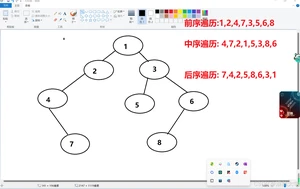
例题4:
设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列是什么?
老样子:如图所示:
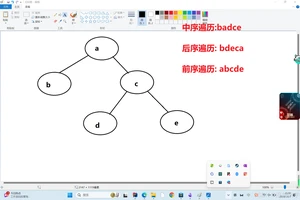
小tips:
如果只给了我们前序序列和后续序列可以创建出二叉树吗?
答案是不可能创建出二叉树的
为什么呢?
因为前序和后序的序列只能够让我们确定这个二叉树的根节点
无法确认这个二叉树的左子树和右子树,所以无法创建二叉树~
本篇到此完结,感谢大家翻阅~
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/h6javajc/25381.html
