java基础教学41讲



1.3.3 级数
1、将这两个方程相减得 $S=frac {1}{2}+frac {1}{2^2}+frac {1}{2^3}+frac {1}{2^4}+frac {1}{2^5}+cdots$ 改为 $S=1+frac {1}{2}+frac {1}{2^2}+frac {1}{2^3}+frac {1}{2^4}+frac {1}{2^5}+cdots$

2.3 要分析的问题
1、“我们定义两个函数$T_{avg}(n)$和$T_{wrost}(n)$，分别为输入为$n$时，算法所花费的平均运行时间和最坏的情况下的运行时间。显然$T_{avg}(n)le T_wrost(n)$。”改为“我们定义两个函数$T_avg(n)$和$T_worst(n)$，分别为输入为$n$时，算法所花费的平均运行时间和最坏的情况下的运行时间。显然$T_{avg}(n)le T_worst(n)$。”

2.4.3 最大子序列和问题的解
1、式（2.2）第一行等号右边分子$(n − i + 1)(n − i)$改为$(n - i + 2)(n - i + 1)$

2.4.4运行时间中的对数
1、1.对分查找 于是循环次数最多为$⌊log (n − 1)⌋+ 2 $

3.5.1 一元多项式
1、同样可以用线性表Q来表示：$Q = [q_0, q_1, q_2, … , q_n]$改为$Q = [q_0, q_1, q_2, … , q_m]$
2、“$P_2(X) = 3X^{1990} - 2X^{1492} + 5$”改为“$P_2(X) = 3X^{1990} - 2X^{1492} +11X+ 5$”

4.2.2 计算后缀表达式的值

1、“把操作符放在两个操作数之间的表达式称为后缀表达式”改为“把操作符放在两个操作数之后的表达式称为后缀表达式”
2、“表4.3列出了后缀表达式abc−/de+”改为“表4.3列出了后缀表达式abc-/de*+”
3、“再看一例，后缀表达式abcd−ef +/+”改为“再看一例，后缀表达式ab*cd−ef+/+”
4、“表4.6 所示为中缀表达式a/(b − c) + de 转换为后缀表达式abc − /de+ 的过程”改为：“表4.6 所示为中缀表达式a/(b − c) + d*e 转换为后缀表达式abc − /de*+ 的过程”
5、表4.6倒数第4行第2列，改为：“ICP(′*′)>ISP(′+′),′*′ 进栈”

4.2.4 利用两个栈计算表达式
1、“因此，可以用语句“printDigit(n/10)”递归地解决它”改为“printOut(n/10)递归地解决它”

4.4.4 循环队列
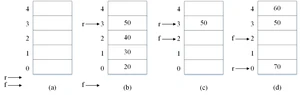
1、“因此60**入位置0”改为“因此70**入位置0”
2、图4.8改为下图：

4.4.6 队列的链接表示

1、图 4.9 链式队列改成下图

5.2.4 带状矩阵
1、“带状矩阵也称为对角矩阵。”删去

5.3 稀疏矩阵的压缩存储
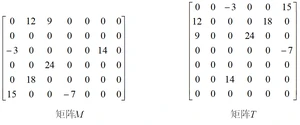
1、图5.7改为下图：

6.1.1 顺序表的查找
1、“例如，查找表中最后一个记录时，需要比较 n 次。”改为“例如，查找表中最后一个记录时，需要比较 1 次；查找表中第一个记录时，则需要比较 n 次”

6.4.1拉链法
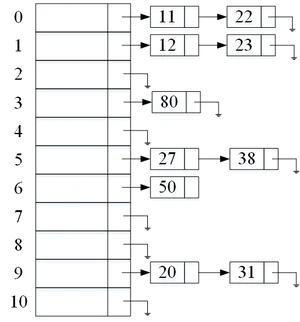
1、第一张图改为下图：

7.4.2 效率分析
1、“从程序7.5 中可以看出，直接选择排序移动次数较少，但关键字的比较次数依然是1/2n(n+1)”改为：“从程序7.5 中可以看出，直接选择排序移动次数较少，但关键字的比较次数依然是1/2n(n-1)”

7.6.2 链式基数排序
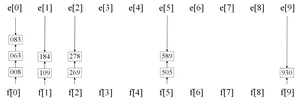
1、图7.10 第三次分配之后 改为下图：

7.7.2 简单算法
1、第2张图里的“51”改为“41”

8.1.1 基本术语
1、“若某节点在第 l 层，则其子孙的根就在第l + 1 层”改为“若某节点在第 l 层，则其子树的根就在第l + 1 层”

8.1.3 树的表示
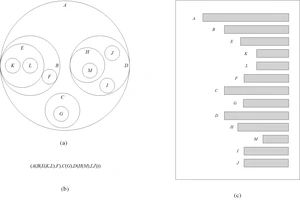
1、图8.2改为下图

8.3.2 二叉树的实现
1、删去该章最后一句话“如图 8.8所示为完全二叉树上节点及其左、右孩子节点之间的关系。”

8.3.4 二叉树的遍历方法以及非递归实现
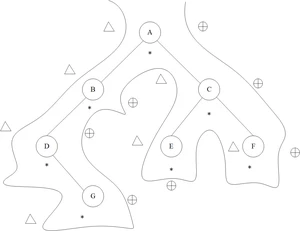
1、图8.9 遍历图的路线示意图改成下图：

2、程序8.15订
在第4行return后加上mQueue.push(node);
第6、7行改成

1
2

TreeNode temp = mQueue.pop();   // 访问队首节点并出队
visit(temp);

并把第14行的mQueue.push(node);去掉
完整程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

public void levelOrder(TreeNode node) {
   SeqQueue mQueue = new SeqQueue();
   if(node == null)
      return;
   mQueue.push(node);
   while(!mQueue.isEmpty()) {
      TreeNode temp = mQueue.pop();  // 访问队首节点并出队
      visit(temp);
      if(temp.left != null)
         // 将队首节点的左孩子节点入队列
         mQueue.push(temp.left);
 java基础教学41讲      if(temp.right != null)
         // 将队首节点的右孩子节点入队列
         mQueue.push(temp.right);
   }
}

3、“中序遍历的非递归算法的实现，只需将前序遍历的非递归算法中的visit(p)移到 mStack.push(p) 和 p=p.left 之间即可”改为“中序遍历的非递归算法的实现，只需将前序遍历的非递归算法中的 visit(p)移到 mStack.pop() 和 p=p.right 之间即可”
4、程序8.17订
在第5行int sign 之后加上

1
2
3

if (node == null)
   return;
p = node;

第24行的p = p.left 改成 p = p.right
完整程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public void nrpostorderTraverse(TreeNode node){
   Stack mStack = new Stack();
   TreeNode p;
   StackObject temp, q;
   int sign;
   if (node == null)
      return;
   p = node;
   while(!(p == null && mStack.empty())) {
      if(p != null) {    // 节点第一次进栈 
          q = new StackObject();
         q.treeNode = p;
         q.flag = 1;
         mStack.push(q);
         p = p.left;
      }
      else {
         temp = mStack.peek();
         p = temp.treeNode;
         sign = temp.flag;
         mStack.pop();
         if(sign == 1) {
            q = new StackObject();
            q.treeNode = p;
            q.flag = 2;
            mStack.push(q);
            p = p.right;
         }
         else {
            visit(p);
            p = null;
         }
      }
   }
}

8.3.5 表达式树
1、 “图 8.10 (a + (bc)) + (((de) + f)g) 的表达式树”改为：图 8.10 “(a + (b*c)) + (((d* e) + f)*g)” 的表达式树
2、则输出将是“abc + def + g+”，它就是后缀表达式 改为： 则输出将是 “abc*+de*f + g*+”，它就是后缀表达式
3、“在我们的例子中，左子树的值”这句话修改为：在我们的例子中，左子树的值是“a+(b*c)”，右子树的值是“((d*e)+f)*g”，因此整个树表示“(a+(b*c))+(((d*e)+f)*g)”。
4、“图8.10 (a+(bc))+(((de) + f)g) 的表达式树”这句图的批注修改为：“图8.10 (a+(b*c))+(((d*e)+f)*g)”的表达式树”
5、“如果我们应用这种策略于上面的树，则输出将是“abc + def +g+””这句话改为：如果我们应用这种策略于上面的树，则输出将是“abc*+de*f+g*+”
6、“第三种遍历策略是先输出运算符，然后递归地输出右子树和左子树。其结果“++abc+defg”是不太常用的前缀（prefix）记法”这句话改为：“第三种遍历策略是先输出运算符，然后递归地输出左子树和右子树。其结果“++a*bc*+*defg”是不太常用的前缀（prefix）记法”
7、图8.11改成下图：

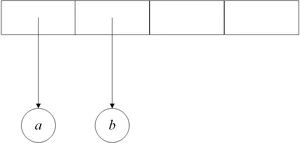
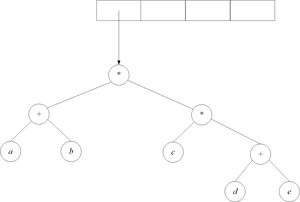
6、图8.14改成下图：

7、图8.15改成下图：

8、图8.16改成下图：

8.3.6 哈夫曼树
1、图8.21 例 8.1 的哈夫曼树改为下图

2、图 8.22 例 8.1 的存储结构改为下图

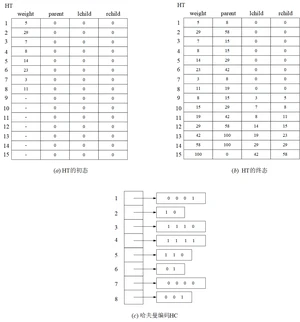
3、图8.23 三元素排列的决策树改为下图

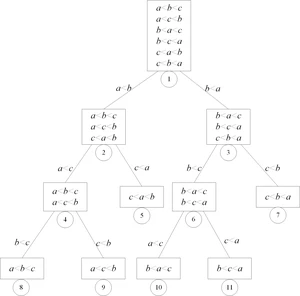
8.5.2 平衡化策略
1、删掉“旋转前，节点k2不满足 AVL平衡特性，因为它的左子树比右子树深 2 层。”
2、 图8.44的名称改为“插入13后的单旋转修复情形（4）”
3、图8.45的名称改为“插入12后的单旋转修复情形（1）”

8.6.3 红黑树的概念
1、图 8.58 红黑树的例子改为下图

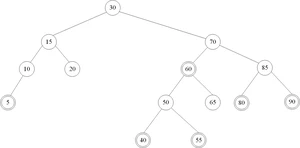
8.6.4 红黑树的实现
图8.61 将45插入图8.58 改为下图：

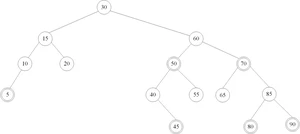
9.4.1 左式堆的性质
1、“证明 由数学归纳法证明。如果 r = 1，则必然至少存在一个树节点。”改为“证明 由数学归纳法证明。如果 r = 1，则必然至少存在一个根节点。”

9.7.2 选择问题
1、“该元素将与第k个最大元素进行比较，记第k个最大元素Sk。注意，Sk是S中最大的元素”改为“该元素将与第k个最大元素进行比较，记第k个最大元素Sk。注意，Sk是S中最小的元素”。

9.7.3 事件模拟
1、“如果有，那么加上这位顾客，处理所需要的统计资料，计算该顾客将要离开的时间”改为“如果有，那么加上这位顾客处理其统计资料的时间，计算该顾客将要离开的时间”。
10.1 图的基本概念
图10.6 改成下图：

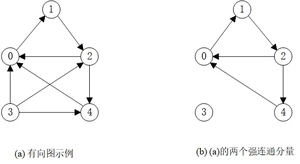
10.4.1 AOV网络
1、“如果有一个非有向无环图”删掉“如果有”

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.bianchenghao6.com/h6javajc/26423.html