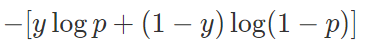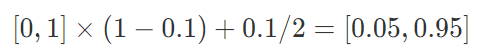Hi，大家好，我是编程小6，很荣幸遇见你，我把这些年在开发过程中遇到的问题或想法写出来，今天说一说
标签平滑的作用_figure标签的作用,希望能够帮助你!!!。

Lable Smoothing
是分类问题中错误标注的一种解决方法。

对于分类问题，特别是多分类问题，常常把向量转换成one-hot-vector（独热向量）
one-hot带来的问题：（对于独热的简单解释：标签平滑Label Smoothing）
对于损失函数，我们需要用预测概率去拟合真实概率，而拟合one-hot的真实概率函数会带来两个问题：
1)无法保证模型的泛化能力，容易造成过拟合；
2) 全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大，而由梯度有界可知，这种情况很难适应。会造成模型过于相信预测的类别。
使用下面的 label smoothing 可以缓解这个问题：

原理：对于以Dirac函数分布的真实标签，我们将它变成分为两部分获得（替换）。

1. 第一部分：将原本Dirac分布的标签变量替换为(1 - ϵ)的Dirac函数；

2. 第二部分：以概率 ϵ ，在u(k) 中份分布的随机变量（u（k）是类别分之一）
   代码：

def label_smoothing(inputs, epsilon=0.1): K = inputs.get_shape().as_list()[-1] # number of channels return ((1-epsilon) * inputs) + (epsilon / K) 

交叉熵（Cross-Entropy）损失函数是分类模型中的一种非常重要的目标函数。在二分类问题中，交叉熵损失函数的形式如下：

如果分类准确，交叉熵损失函数的结果是0（即上式中p和y一致的情况），否则交叉熵为无穷大。也就是说交叉熵对分类正确给的是最大激励。换句话说，对于标注数据来说，这个时候我们认为其标注结果是准确的（不然这个结果就没意义了）。但实际上，有一些标注数据并不一定是准确的。那么这时候，使用交叉熵损失函数作为目标函数并不一定是最优的。

对于这个问题，我们还可以这么去理解。在分类任务中，我们通常对类别标签的编码使用[0,1,2,…]这种形式。在深度学习中，通常在全连接层的最后一层，加入一个softmax来计算输入数据属于每个类别的概率，并把概率最高的作为这个类别的输入，然后使用交叉熵作为损失函数。这会导致模型对正确分类的情况奖励最大，错误分类惩罚最大。如果训练数据能覆盖所有情况，或者是完全正确，那么这种方式没有问题。但事实上，这不可能。所以这种方式可能会带来泛化能力差的问题，即过拟合。

在2016年，Szegedy等人提出了inception v2的模型（论文：Rethinking the inception architecture for computer vision.）。其中提到了Label Smoothing技术，用以减轻这个问题。
我们先来看一下原理。假设我们的分类只有两个，一个是猫一个不是猫，分别用1和0表示。Label Smoothing的工作原理是对原来的[0 1]这种标注做一个改动，假设我们给定Label Smoothing的值为0.1：

可以看到，原来的[0,1]编码变成了[0.05,0.95]了。这个label_smoothing的值假设为ϵ，那么就是说，原来分类准确的时候，p=1，不准确为p=0，现在变成了p=1−ϵ和ϵ，也就是说对分类准确做了一点惩罚。

Label Smoothing在很多问题上对模型都有一定的提升。
在Tensorflow中使用方法时候只要在损失函数中加上label_smoothing的值即可，如下：

tf.losses.softmax_cross_entropy( onehot_labels, logits, weights=1.0, label_smoothing=0, scope=None, loss_collection=tf.GraphKeys.LOSSES, reduction=Reduction.SUM_BY_NONZERO_WEIGHTS ) 

参考：
【1】https://blog.csdn.net/neveer/article/details/
【2】https://www.datalearner.com/blog/44661

今天的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。