柯西变异算子_自适应算法应用实例
Hi,大家好,我是编程小6,很荣幸遇见你,我把这些年在开发过程中遇到的问题或想法写出来,今天说一说
柯西变异算子_自适应算法应用实例,希望能够帮助你!!!。
文章目录
- 一、理论基础
-
- 1、蝴蝶优化算法
- 2、改进的蝴蝶优化算法
-
- (1)柯西变异
- (2)自适应权重
- (3)动态切换概率策略
- (4)算法描述
- 二、函数测试与结果分析
- 三、参考文献
一、理论基础
1、蝴蝶优化算法
请参考这里。
2、改进的蝴蝶优化算法
为了改进蝴蝶算法容易陷入局部最优和收敛精度低的问题,本文从三个方面对蝴蝶算法进行改进。首先通过引入柯西分布函数的方法对全局搜索的蝴蝶位置信息进行变异,提高蝴蝶的全局搜索能力;其次通过引入自适应权重因子来提高蝴蝶的局部搜索能力;最后采用动态切换概率 p p p平衡算法局部搜索和全局搜索的比重,提升了算法的寻优性能。因此本文提出一种混合策略改进的蝴蝶优化算法(CWBOA)。
(1)柯西变异
针对蝴蝶优化算法易陷入局部最优的特点,利用柯西变异来增加种群的多样性,提高算法的全局搜索能力,增加搜索空间。柯西分布函数在原点处的峰值较小但在两端的分布比较长,利用柯西变异能够在当前变异的蝴蝶个体附近生成更大的扰动从而使得柯西分布函数的范围比较广,采用柯西变异两端分布更容易跳出局部最优值。本文融入柯西算子,充分利用柯西分布函数两端变异的效果来优化算全局最优个体,使得算法能够更好地达到全局最优。
在求得当前最优解后,本文使用公式 (1)所示的更新公式对当前全局最优解进行变异处理。 x n e w b e s t = x b e s t + x b e s t × Cauchy ( 0 , 1 ) (1) x_{newbest}=x_{best}+x_{best}×\text{Cauchy}(0,1)\tag{1} xnewbest=xbest+xbest×Cauchy(0,1)(1)
(2)自适应权重
自适应权重公式如式(2)所示 w = s i n ( π t 2 ⋅ i t m a x + π ) + 1 (2) w=sin(\frac{\pi t}{2\cdot itmax}+\pi)+1\tag{2} w=sin(2⋅itmaxπt+π)+1(2)其中, t t t为当前迭代次数, i t m a x itmax itmax为最大迭代次数。
改进后的局部搜索公式为 x i t + 1 = w ⋅ x i t + ( r 2 × x j t − x k t ) × f i (3) x_i^{t+1}=w\cdot x_i^t+(r^2×x_j^t-x_k^t)×f_i\tag{3} xit+1=w⋅xit+(r2×xjt−xkt)×fi(3)通过融合自适应权重因子 w w w,使蝴蝶个体具有更好的局部寻优能力。
(3)动态切换概率策略
引入动态切换概率来平衡局部开采和全局开采的比重,来实现更好的寻优策略。动态切换概率 p p p的公式如下 p = 0.6 − 0.1 × ( M a x I t e r − t ) / M a x I t e r (4) p=0.6-0.1×(MaxIter-t)/MaxIter\tag{4} p=0.6−0.1×(MaxIter−t)/MaxIter(4)
(4)算法描述
CWBOA的具体执行步骤如下:
图1 改进算法的流程图
二、函数测试与结果分析
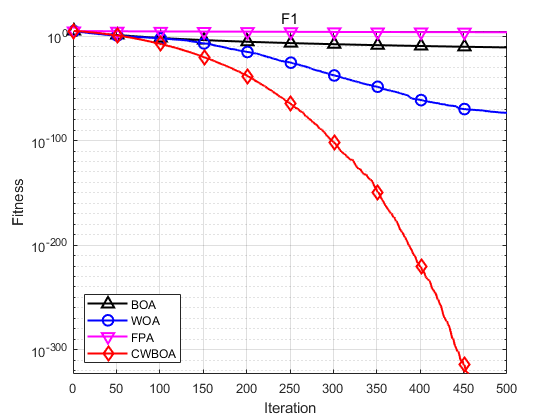
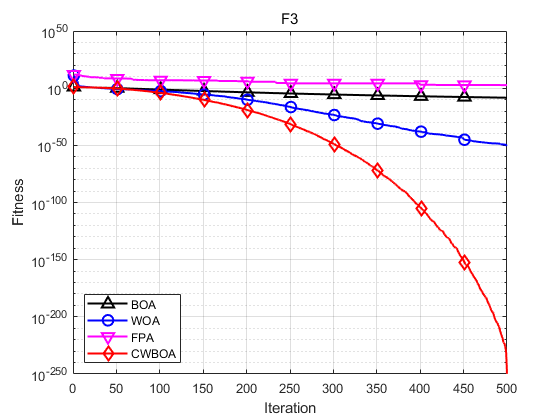
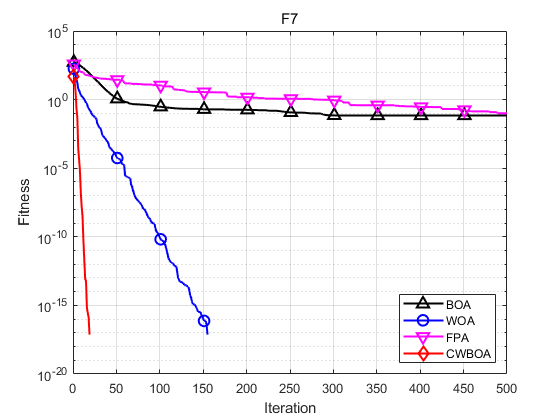
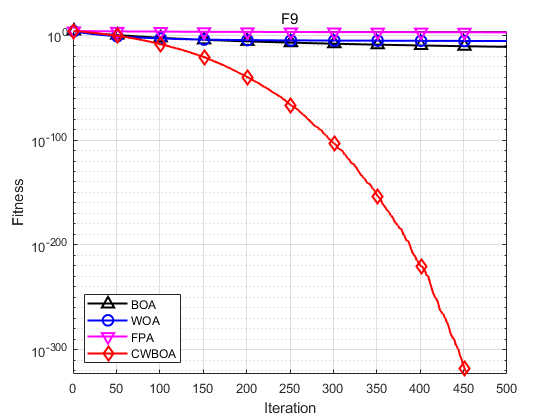
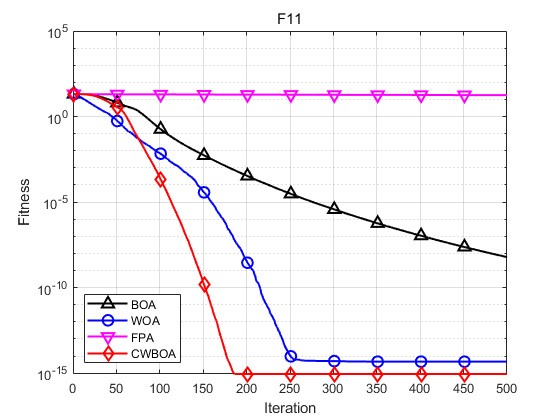
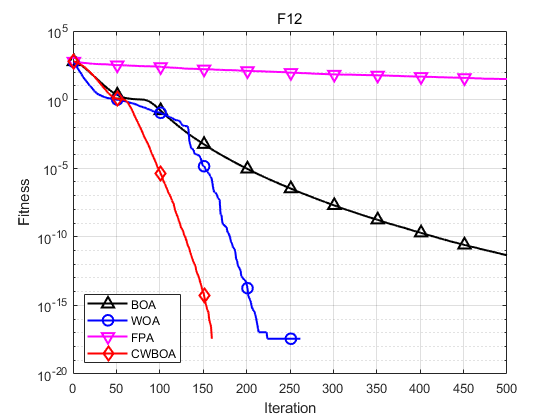
本文选取了基于柯西变异和动态自适应权重的蝴蝶优化算法(CWBOA) 、基本蝴蝶算法 (BOA)、鲸鱼算法(WOA)以及花授粉算法(FPA)进行对比。为了实验的公平、客观性,本文将所有算法的初始种群规模统一设为30, 迭代次数设置为500,四个算法的共有参数保持一致。CWBOA和BOA 中的 c c c感官形态设置为0.01, a a a幂指数在迭代过程从0.1迭代到0.3;基本的BOA和FPA中的切换概率均为 p = 0.8 p=0.8 p=0.8。
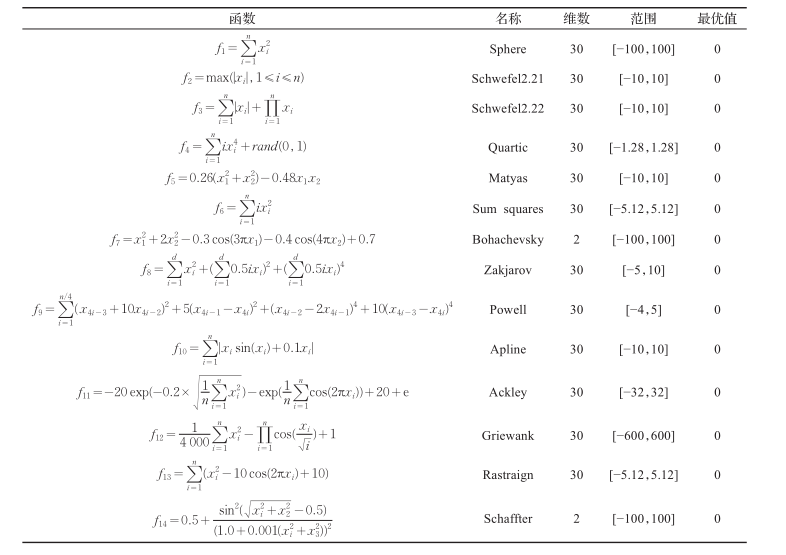
为了验证改进后的BOA在收敛性和鲁棒性两方面的性能上更优,本文基于14个测试函数进行对比实验,标准测试函数的信息见表1。
表1 测试函数的基本信息
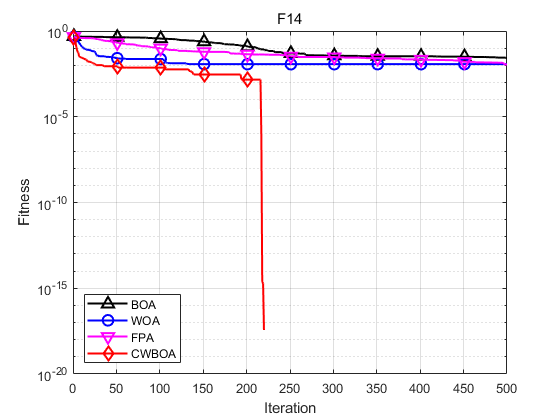
函数:F1 BOA:最大值: 1.4499e-11,最小值:1.1241e-11,平均值:1.2801e-11,标准差:8.858e-13 WOA:最大值: 7.3975e-73,最小值:2.3916e-85,平均值:3.131e-74,标准差:1.353e-73 FPA:最大值: 23803.0104,最小值:947.6602,平均值:4173.2952,标准差:5457.3121 CWBOA:最大值: 0,最小值:0,平均值:0,标准差:0 函数:F3 BOA:最大值: 5.7184e-09,最小值:2.2932e-09,平均值:4.4704e-09,标准差:1.278e-09 WOA:最大值: 8.9851e-50,最小值:4.8473e-58,平均值:5.076e-51,标准差:1.8277e-50 FPA:最大值: 8710.4476,最小值:28.1287,平均值:513.6911,标准差:1768.5884 CWBOA:最大值: 4.7981e-249,最小值:7.7934e-279,平均值:1.6759e-250,标准差:0 函数:F7 BOA:最大值: 0.41445,最小值:1.7408e-13,平均值:0.068926,标准差:0.15676 WOA:最大值: 0,最小值:0,平均值:0,标准差:0 FPA:最大值: 2.755,最小值:2.959e-11,平均值:0.10097,标准差:0.50222 CWBOA:最大值: 0,最小值:0,平均值:0,标准差:0 函数:F9 BOA:最大值: 1.2352e-11,最小值:8.7385e-12,平均值:1.012e-11,标准差:1.0014e-12 WOA:最大值: 5.2454e-05,最小值:1.6577e-46,平均值:4.0482e-06,标准差:1.0357e-05 FPA:最大值: 3505.7816,最小值:70.2088,平均值:711.0633,标准差:1036.3243 CWBOA:最大值: 0,最小值:0,平均值:0,标准差:0 函数:F11 BOA:最大值: 6.6915e-09,最小值:5.2465e-09,平均值:6.057e-09,标准差:3.692e-10 WOA:最大值: 7.9936e-15,最小值:8.8818e-16,平均值:4.6777e-15,标准差:2.6279e-15 FPA:最大值: 19.9631,最小值:14.2613,平均值:17.6983,标准差:1.6073 CWBOA:最大值: 8.8818e-16,最小值:8.8818e-16,平均值:8.8818e-16,标准差:0 函数:F12 BOA:最大值: 7.7948e-12,最小值:8.4921e-13,平均值:4.5165e-12,标准差:2.1098e-12 WOA:最大值: 0,最小值:0,平均值:0,标准差:0 FPA:最大值: 223.7537,最小值:9.77,平均值:31.449,标准差:40.2159 CWBOA:最大值: 0,最小值:0,平均值:0,标准差:0 函数:F14 BOA:最大值: 0.043863,最小值:7.9381e-14,平均值:0.026527,标准差:0.021455 WOA:最大值: 0.043671,最小值:0,平均值:0.011645,标准差:0.019642 FPA:最大值: 0.047395,最小值:8.7206e-05,平均值:0.011072,标准差:0.015677 CWBOA:最大值: 0,最小值:0,平均值:0,标准差:0 由函数的收敛曲线可知,改进的CWBOA在收敛的速度和精度上要优于BOA、WOA、FPA。
三、参考文献
[1] 高文欣, 刘升, 肖子雅, 等. 柯西变异和自适应权重优化的蝴蝶算法[J]. 计算机工程与应用, 2020, 56(15): 43-50.
今天的分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
上一篇
已是最后文章
下一篇
已是最新文章