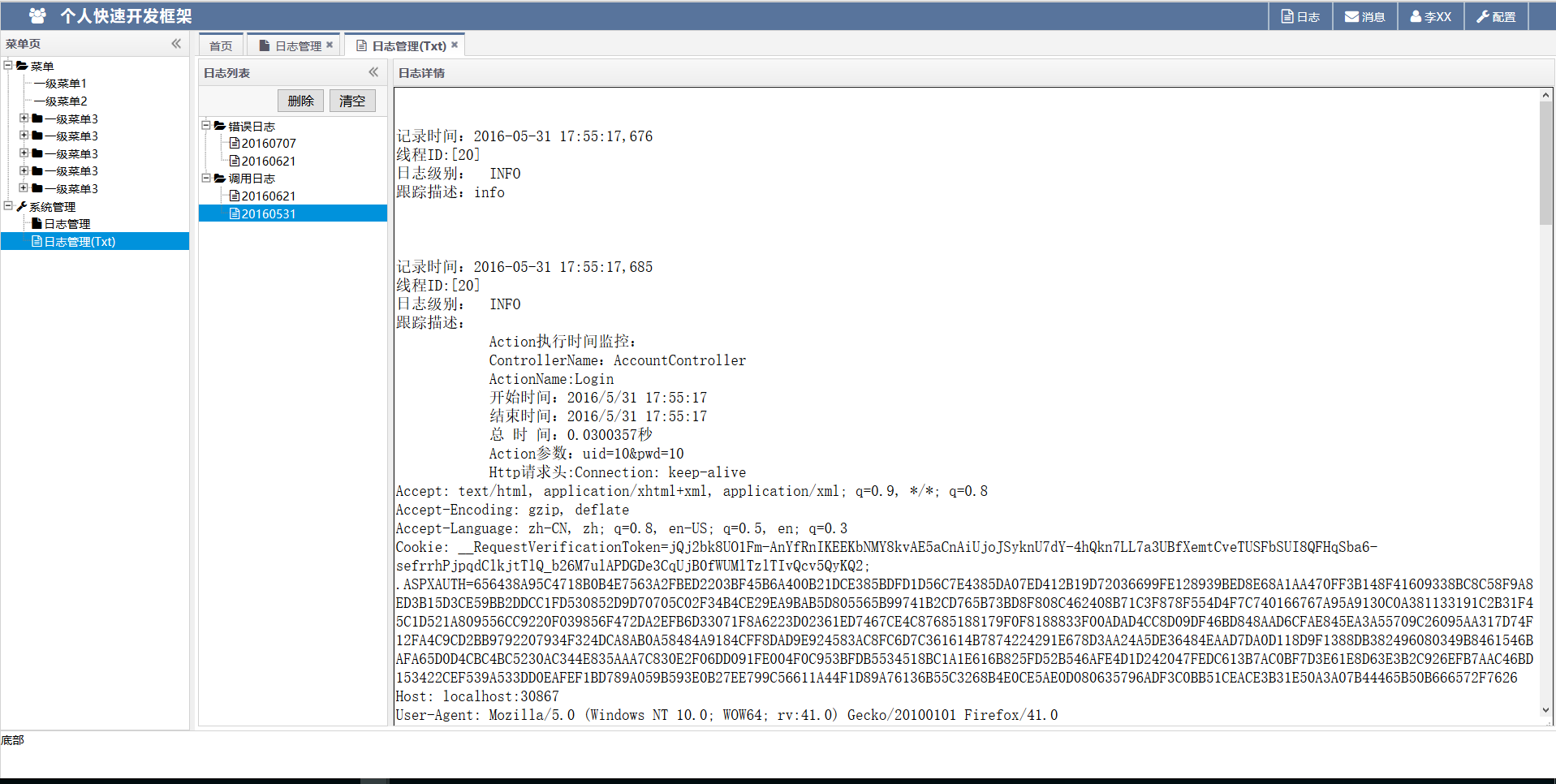
Booth 算法_booth算法乘法例题讲解
Hi,大家好,我是编程小6,很荣幸遇见你,我把这些年在开发过程中遇到的问题或想法写出来,今天说一说
Booth 算法_booth算法乘法例题讲解,希望能够帮助你!!!。
综述
记一次介绍Booth 算法思想的答疑.
正文
Here I give the idea and explanation of the algorithm.
First, let me introduce the idea:
Consider the multiplication of 1101(multiplicand) and 1110 (multiplier).
In this process, you may notice that if the current bit in the multiplier is 0 there are 4 zeros. (Yellow box)
If the current bit is 1, we need to add multiplicand (1101) to the current result. (Red box)
If a multiplier has many non-zero bits 10, then the number of operations will be more (we do not like this : | )
The Booth algorithm solves this problem well. Since addition will multiply so many times, why not use subtraction. Actually, the above 1110 can be written as 10000-10, then you can get the result by multiplying twice (note there are only two 1s) and then do subtracting, so this is the principle of Booth’s algorithm.
Then, let me explain how the algorithm is derived.
As you can see here
1110 = 01110 = (10000 - 10)
So how can we get this transformation easily?
Just consider a general case:
For this multiplier, there are n bits of 1, followed by m bits of 0.
You can write down the transformation like this:
The grey one is equal to the blue one minus the red one.
To get the blue one, all you need is 1 and (n+m) bits zeros.
To get the orange one, all you need is 1 and (m) bits zeros.
We know for the blue, we will add multiplicand at the current position, for the red one we need to do subtraction.
Then how can we identify this in CPU?
Let’s see the number again: (here I just add one zero in front of the number. This will not influence the value.)
You can identify the number by identifying 0-1 and 1-0 transitions.
Let’s go back to this problem.
Recall The Booth algorithm solves this problem well. Since addition will multiply so many times, why not use subtraction. Actually, the above 1110 can be written as 10000-10, then you can get the result by multiplying twice (note there are only two 1s) and then do subtracting, so this is the principle of Booth’s algorithm.
For 1101(multiplicand) and 1110 (multiplier), suppose now, you identified 0-1 transition, then you know you need to do the subtraction, then get 2’s complement.
Similarly, when you identify the 1-0 transition, you need to do addition.
During this process, do not forget the shift to make sure when we perform operations, these bits are aligned.
Hope this helps!
Further, I suggest you derive it by yourself, and you will experience the beauty of this algorithm.
今天的分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
上一篇
已是最后文章
下一篇
已是最新文章