Hi，大家好，我是编程小6，很荣幸遇见你，我把这些年在开发过程中遇到的问题或想法写出来，今天说一说杨辉三角的python代码_杨辉三角计算公式,希望能够帮助你!!!。

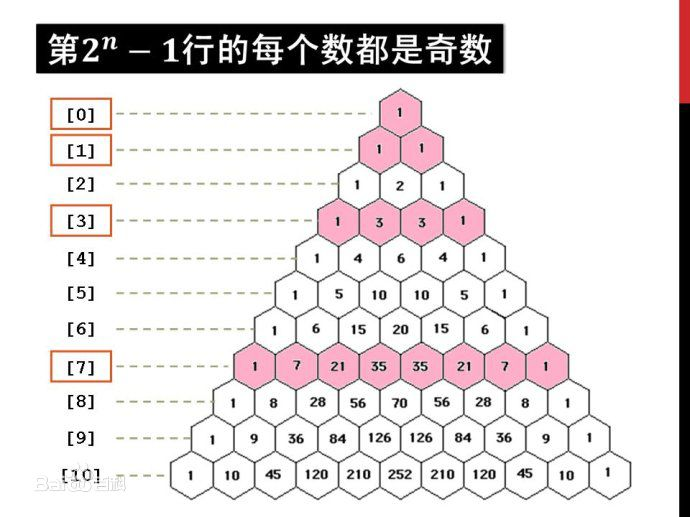
杨辉三角的基本概念

杨辉三角，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现

特点

1. 每个数等于它上方两数之和。
2. 每行数字左右对称，由1开始逐渐变大。
3. 第n行的数字有n项。
4. 第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
5. 第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。
6. 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
7. (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
8. 将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。

Python的三种实现方法

方法一

• 将杨辉三角每次计算时，都抽象成每行后面先增加一个0

• 于是本行第i个元素就等于上一行的(i-1)个元素和i元素的和（每行第0个元素是上一行抽象后的第0个元素和第(0-1)个元素，即抽象出来的0与1的和）

• 抽象出来的0为下一行提供足够的遍历次数

  [1, 0]
  [1, 1, 0]
  [1, 2, 1, 0]
  [1, 3, 3, 1, 0]
  [1, 4, 6, 4, 1, 0]
  

代码：

def triangles():
    row = [1]
    while True:
        yield row
        row.append(0)  # 补零以便于计算下一行数据
        row = [row[i - 1] + row[i] for i in range(len(row))]  # 通过本行相邻两个数据相加获得下一行的数据


if __name__ == '__main__':
    t = triangles()
    for i in range(6):
        print(next(t))

结果：

[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]

方法二

• 循环内的遍历从1开始，即从代码开头定义每行的初始值为1，后续不再改变
• 由第二个元素开始，每行元素为上一行对应位置和前一位置元素的和
• 每行最后一个元素都为1，直接最后添加即可

代码：

def triangles():
    row = [1]
    while True:
        yield row
        for i in range(1, len(row)):
            row[i] = pre_line[i] + pre_line[i - 1]  # 本行第 i 个元素为上一行的 i 元素与 i-1 元素相加
        row.append(1)  # 本行最后需要补元素 1
        pre_line = row[:]  # 复制本行, 用于计算下一行数据


if __name__ == '__main__':
    t = triangles()
    for i in range(6):
        print(next(t))

结果：

[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]

方法三

• 此方法相对较复杂，它在列表内嵌套列表形成二维列表，杨辉三角的每行为二维列表的一个列表元素
• 函数遍历杨辉三角的每一行，单独计算该行的每一个元素，其中每个元素为上一行同位置的元素和前一个元素之和
• 上一行元素在函数中表现为二维列表的前一个元素
• 该行首尾计算时，分别抽象为前后多一个零进行计算

代码：

def triangles (line):
    result = [[1]]
    for row in range(1, line):  # for 循环计算杨辉三角一共多少行
        current_row = []
        for column in range(row+1):  # for 循环计算当前行一共多少个元素
            if column == 0:
                upper_former_param = 0  # 计算此行的第一个元素, 则它上一行的前一个元素为 0
            else:
                upper_former_param = result[row-1][column-1]  # 获得此行元素在上一行的前一个元素

            if column == len(result[row-1]):
                upper_param = 0  # 计算此行的第一个元素, 则它上一行同样位置的元素为 0
            else:
                upper_param = result[row-1][column]  # 获得此行元素在上一行同样位置的元素

            param = upper_former_param + upper_param  # 此行的元素为上一行同样位置及其前一个位置的和
            current_row.append(param)  # 将该元素添加到这一行
        result.append(current_row)  # 将这一行添加到结果中
    return result


if __name__ == '__main__':
    print(triangles(6))

结果：

[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]]

今天的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。